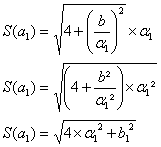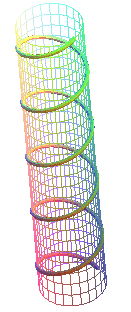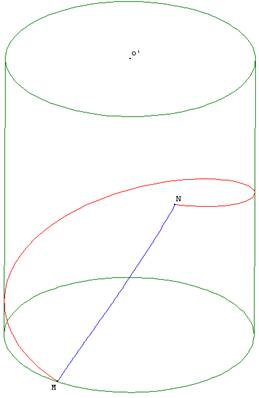
Le chemin le plus court sur le cylindre

Le plus court chemin d’un point A à un point B sur une surface développable est la ligne droite reliant les deux points sur le patron du solide. Ainsi le plus court chemin d’un point à un autre sur le cylindre une droite sur le patron, mais comment la représenter en trois dimensions ? Nous disposons de l’équation paramétrable de l’hélice cylindrique. Nous nous proposons de démontrer que l’hélice est le chemin le plus court. 

Équation de l’hélice 1, la bleue sur le schéma (elle est dire « dextre » : elle monte dans le sens trigonométrique et un observateur placé à l’extérieur la voit, lorsqu'il est devant, monter de gauche à droite) :            

Équation de l’hélice 2, la rouge sur le schéma (elle est dite « senestre » : elle monte dans le sens des aiguilles d’une montre) :

L’une des deux hélices est toujours la plus courte si elle représente une droite sur son patron. Pour le prouver, calculons la longueur de l’hélice et comparons la longueur obtenue à la longueur du segment AB sur le patron.

Longueur de l’hélice cylindrique

On obtient :

En remplaçant par les valeurs que nous avons utilisées dans GeoSpace, nous obtenons :

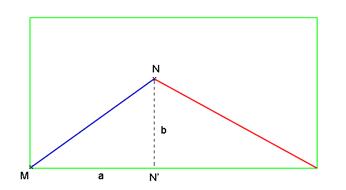
S(a₁) correspond à la longueur de l’hélice sur le cylindre.

Longueur de la droite MN sur le patron

Calculons maintenant la longueur du plus court chemin, la droite sur le patron.

 avec r le rayon du cercle et a₁ l’angle MON’.

On a avec le théorème de Pythagore :

Pour  on a

Quel est donc le chemin le plus court ?

On remarque bien sûr que la longueur de l’hélice cylindrique est la même que la droite sur le patron. Le chemin le plus court en deux dimensions est une droite qui correspond à une hélice bien spécifique dans trois dimensions.

Hélice senestre                                                                 Hélice dextre

© 2003 Matthieu Aubry - Pascal Blome
Le contenu est disponible selon les termes de la licence GNU Free Documentation License.