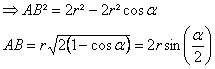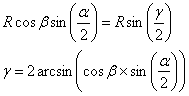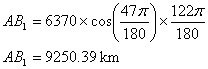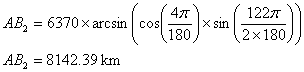|
|||||||||||

|
Le chemin le plus court sur la sphèreAprès avoir étudié le cas du chemin le plus court sur des surfaces développables (cube et cylindre), nous nous proposons de déterminer la plus courte distance sur une surface plus complexe : la sphère. Comment déterminer le plus court chemin entre deux points A et B sur une sphère quelconque ? Quel trajet doit emprunter un avion effectuant le vol Poitiers-Seattle ?
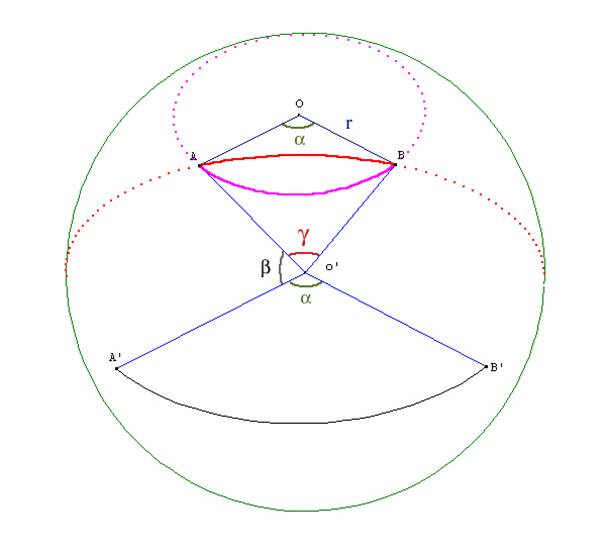
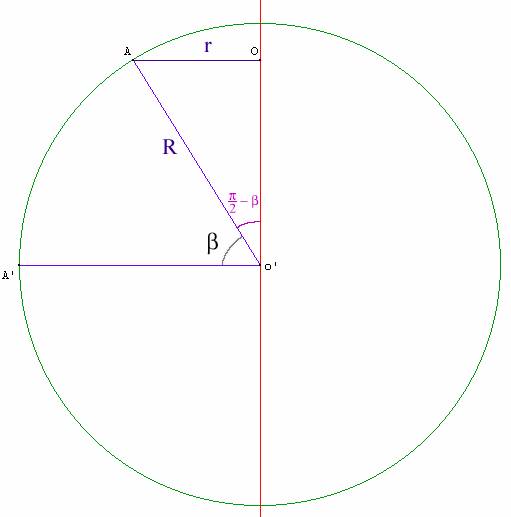
Schéma 1 Pour effectuer la distance AB, trois solutions sont envisageables : - on trace la parallèle à l’équateur passant par A et B avec pour centre O - on trace le cercle passant par A, B et dont le centre est le point O’, centre de la sphère. Ce cercle est appelé « grand cercle » - on trace une distance aléatoire quelconque Nous ne traiterons pas la troisième possibilité car elle apparaît forcément plus longue que les deux premières. Traitons donc les deux premiers cas successivement, et démontrons lequel est le chemin le plus court. Distance AB sur la parallèle à l’équateur
Schéma 2
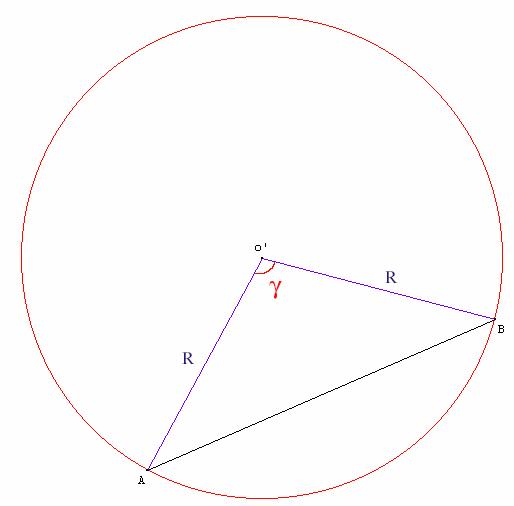
Nous avons donc calculé la distance AB1, représentée en violet sur le schéma 1. Distance AB sur le grand cercle passant par A et BPour calculer la distance AB sur le grand cercle (représentée en
rouge), il faut calculer la valeur de l’angle g. Comme l’on connaît la
valeur de r, il suffira de calculer
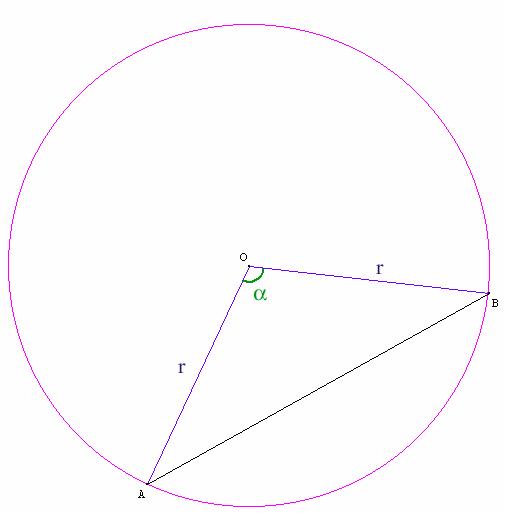
Schéma 3 Avec le théorème d’Al Kashi
dans le triangle ABO :
Schéma 4 On cherche g avec Al Kashi :
Nous avons donc calculé la
distance AB2, représentée en rouge
sur le schéma 1. Quel est le chemin le plus court ?Il s’agit maintenant de déterminer le chemin le plus court entre la distance AB1 et la distance AB2. Pour cela nous avons choisi de calculer les 2 distances séparément pour deux villes sur le globe terrestre :
Rayon terre : 6370 km
AB1 > AB2 AB1 - AB2 = 9250.39 – 8142.39 = 1108 km Ainsi la distance AB2 qui correspond à la distance AB sur le grand cercle est largement inférieure à la distance AB1 : plus de 1108km de différence ! Voici les deux distances représentées graphiquement sur un globe vu de haut :
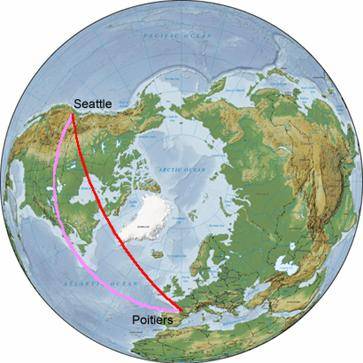
Comparaison des deux
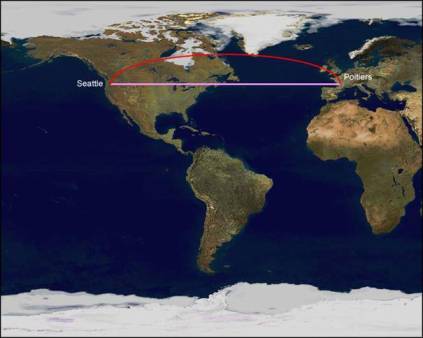
distances sur un globe Quel serait le résultat d’un tel tracé sur un planisphère ? Le chemin le plus court serait-il la ligne droite allant de Poitiers vers Seattle, comme le pensent beaucoup de personnes ?
Comparaison des deux
distances sur un planisphère La sphère n'est pas un solide développable : une écorce d'orange éclate si on la plaque sur un plan et une feuille de papier se froisse sur une sphère. Donc les distances sur la sphère ne peuvent être reportées exactement sur un plan. Ceci explique que le tracé du plus court chemin en 3 dimensions ne correspond pas au tracé du plus court chemin dans un espace en 2 dimensions. Toutes les cartes de type planisphère sont donc fausses ! De plus, nous avons contacté un responsable des trajets d’Air France qui nous a longuement expliqué le fonctionnement et la mise en place des chemins empruntés par les avions chaque jour. Il a d’ailleurs été étonné par la précision de notre calcul ! En effet il n’y avait que très peu de différences avec les plans de vol. Les différences s’expliquent selon lui suite à des facteurs externes : le vent, les turbulences (et la météo en général), le poids de l’avion, les routes parfois imposées au dessus de certains Etats, etc. Cette prise de contact fut réellement enrichissante car elle a pu confirmé la justesse de cette démonstration ! Conséquences d’une telle démonstration ?Quelles conséquences un tel calcul peut-il avoir sur les transports, l’environnement et la société en général ? Sachant qu’un Boeing 747 vole en moyenne à 970km/h et consomme 15t/h, il parcourt 1108km en 1h09 consommant alors 17 tonnes de kérosène ! Nous pouvons donc en conclure que sur un trajet tel que Poitiers-Seattle aller retour, emprunter le chemin le plus court plutôt que le chemin parallèle à l’équateur fait économiser 34T de carburant, soit 107T de CO2 de moins de dégagées dans l’atmosphère… minimisant un bilan déjà très lourd pour l’environnement (plus de 10 millions de T de kérosène brûlées chaque jour). Les conséquences sont donc gigantesques pour les communications et
les transports : un temps immense est gagné sur toutes les distances
parcourues. La dégradation de l’environnement est de plus limitée, ce qui
permet de mettre en avant l’utilité des mathématiques dans un tel
domaine !
| ||||||||||