|
||||||||

|
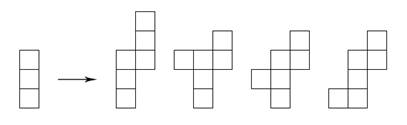
Le chemin le plus court sur le cubeLe cube étant un espace euclidien, nous savons que le chemin plus court d’un point à un autre est la droite qui relie ces deux points sur son patron. Il existe en tout 11 patrons du cube (voir ci-dessous) : la difficulté est donc de choisir le bon patron pour déterminer le chemin le plus court. Comment trouver les patrons du cube ?Les patrons sont constitués des six faces du cube et peuvent être obtenus en 3 étapes successives.
On sait qu’on ne peut aligner plus de quatre bases, sinon une face serait présente en double. On aligne donc quatre carrés et on dispose les deux derniers sur les côtés.
On obtient les 6 premiers patrons. Si on s'interdit d'aligner plus de trois carrés on découvre alors quatre nouveaux patrons.
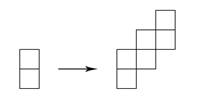
On trouve le dernier patron en alignant seulement deux carrés (le minimum possible),
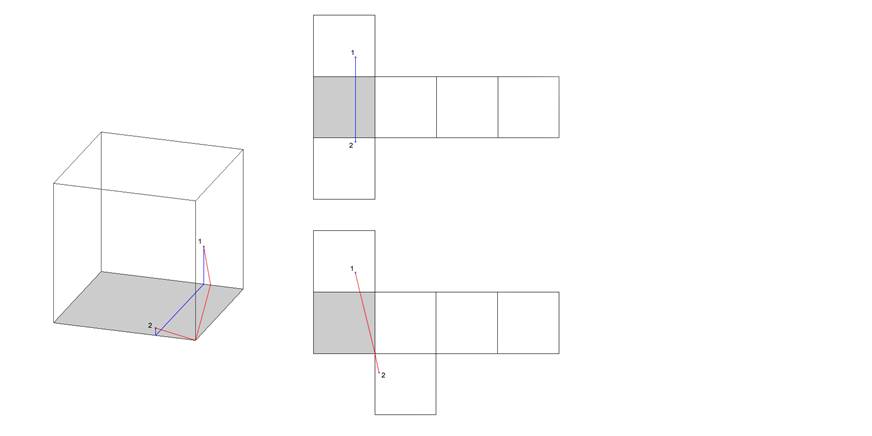
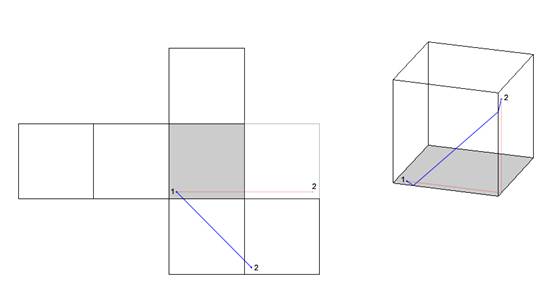
Il n'y a pas d’autres solutions possibles. Quel patron faut-il choisir pour relier deux points par le plus court chemin ?Il n’y a que deux possibilités pour placer deux points sur un cube : soit sur des faces opposées, soit sur des faces adjacentes. Traitons les deux cas successivement. 1) Deux points sur des faces opposéesSi les points se trouvent sur des faces opposées il y a quatre chemins possibles utilisant chacun au moins 3 faces alignées. Traitons dans un exemple les deux cas les plus probables. Exemple n°1
Longueurs Trajet
bleu : 0,82 Trajet
rouge : 1,00 Il existe deux possibilités envisageables pour tracer le plus court chemin reliant les deux points : le trajet bleu utilisant 3 faces, et le rouge qui en utilise 4. Selon la position des points l’un est plus court que l’autre. La seule solution est donc de les mesurer. 2) Deux points sur des faces adjacentesSi les points se trouvent sur des faces adjacentes les solutions sont plus difficiles à trouver, car il faut considérer plus de solutions possibles en fonction de la position des points sur la face. En général elles se trouvent sur un des deux patrons partiels suivants (voir exemples) en choisissant la bonne base. Exemple n°2
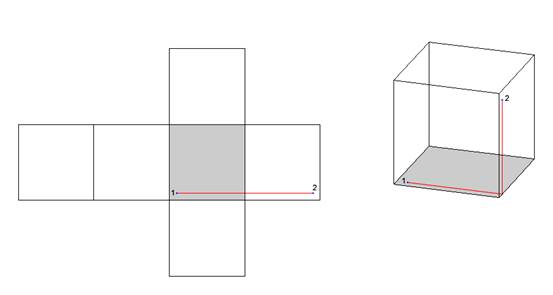
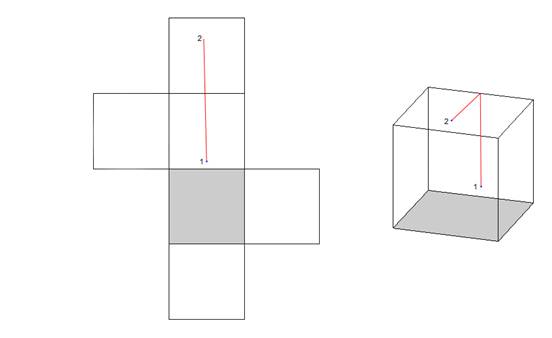
Ici nous voyons bien que le chemin qui relie les points 1 et 2 n’est pas le plus court. Sur ce patron néanmoins un seul tracé est possible. Nous devons donc utiliser un autre patron.
Longueurs Trajet
rouge : 1,00 Trajet
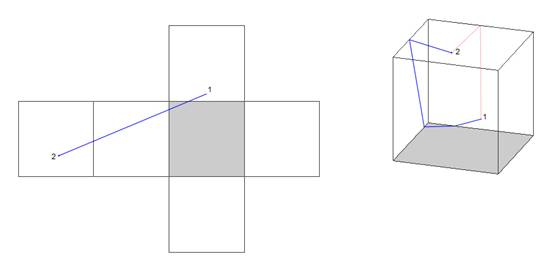
bleu : 0,80 Nous voici devant un tracé plus avantageux. Le chemin bleu est bien plus court que le rouge, et cela même s’il utilise trois faces au lieu de deux. Ceci montre bien qu’il existe deux possibilités pour trouver le chemin le plus court sur deux faces adjacentes : soit sur deux faces, soit sur trois faces, en angle. Exemple n°3
Longueurs Trajet
rouge : 0,76 Trajet
bleu : 1,00 Il est facile de voir que le chemin rouge est largement plus court que le bleu. En effet, le chemin bleu emprunte un trajet inutile, et beaucoup plus long : 4 carrés contrairement au rouge qui n’en n’utilise que 2. Existe-t-il une méthode ?Pour relier deux points par le chemin le plus court, il faut donc observer le cube et choisir les faces qui conviennent. Il n’y a pas de véritable méthode pour définir le chemin le plus court : il faut donc tester les solution les plus probables, en éliminant préalablement les autres solutions (comme le trajet bleu ci-dessus qui au premier coup d’œil paraît beaucoup plus long que le rouge). La recherche du plus court chemin sur le cube se limite donc au tracé et à la mesure des différentes possibilités de trajets. On ne peut en déduire une règle fonctionnelle, car le patron à utiliser dépend des placements des points sur les faces, il existe donc des centaines de possibilités !
| |||||||