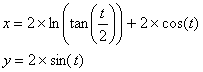|
||

|
La géométrie non euclidienneNous venons d’étudier le cas de la sphère. Sur une sphère, la somme des angles d’un triangle est forcément supérieure à 180°. Mais depuis notre tendre enfance nos professeurs ne nous ont-ils pas enseigné que la somme des angles d’un triangle est forcément égale à 180° ? Comment expliquer cette contradiction ? Existe-t-il d’autres géométries ne répondant pas aux principales règles énoncées par Euclide ? Dans ces cas éventuels, la ligne droite peut-elle être le chemin le plus court ? Un cercle… infini ?
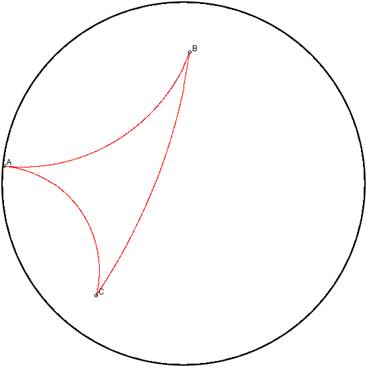
Distances : AB=7,85 AC=7,43 BC=3,88 Angles : BAC=0,4° ABC=13,1° ACB=20,4° Cette simulation nous met bien devant un gros problème semblant inexplicable : les droites sont courbées, la somme des angles fait environ 34° et les distances ne correspondent pas aux mesures géométriques ! Pourtant on nous a toujours enseigné que la somme des angles d’un triangle faisait 180°, et une droite ne peut pas être courbé ; quant aux distances, comment une droite plus longue peut-elle être plus courte ? La réponse : la géométrie non-euclidienne. Le schéma ci-dessus est une modélisation d’un monde en deux dimensions, un cercle, répondant à une simple exigence : lorsqu’on s’approche du bord la pression augmente, les objets deviennent plus petits, ainsi que les droites qui deviennent alors courbes. Le bord a une pression infinie et ne peut être atteint qu’en théorie par des êtres vivant sur ce monde. Si nous choisissons ‘R’ comme rayon fini du cercle et ‘r’ la distance d’un point au centre de celui-ci, nous disons que la pression est proportionnelle à ‘R²-r²’. Cette équation a été établie par Henri Poincaré, célèbre mathématicien de notre siècle. C’est le père de la géométrie non-euclidienne, une invention abstraite de mathématiciens afin de répondre à certaines exigences, notamment de la théorie de la relativité et de la physique quantique. Le but est de quitter les représentations ordinaires des choses et inventer une géométrie en conséquence. Il dit dans son livre L’espace et la géométrie (1908) : « Si l'espace géométrique était un cadre imposé à chacune de nos représentations, […] il serait impossible de se représenter une image dépouillée de ce cadre, et nous ne pouvons rien changer à notre géométrie. Mais il n'en est pas ainsi […] ». Il enchaîne alors avec l’exemple dont nous avons parlé précédemment et imagine comment des êtres vivant dans un tel espace pourraient se représenter la géométrie : en supposant que la lumière qui traverserait ce monde soit également influencée par la pression « de telle sorte que l'indice de réfraction soit inversement proportionnel à ‘R²-r²’ » (elle serait alors courbée tout comme les droites), cela compenserait donc la vision des choses tel que nous les voyons. Les êtres établiraient donc une géométrie différente de la notre, mais adapté à leur monde : 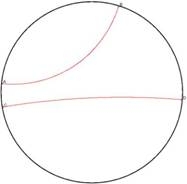 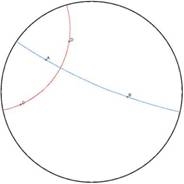 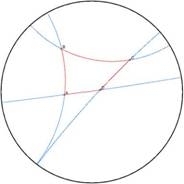
Une
parallèle Une
perpendiculaire Un
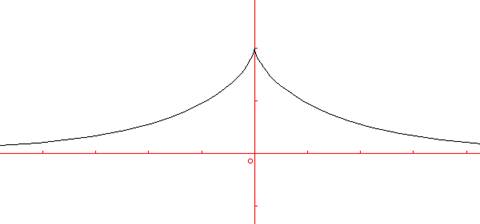
quadrilatère Cette modélisation a pour but de montrer que le monde dans lequel nous vivons n’est certainement pas celui que nous croyons être. Qu’est-ce qui nous prouve que notre monde ne répond pas à de telles exigences, dont nous ne pouvons être que les acteurs innocents, impuissants… et ignorants ? La géométrie de LobatchevskiLobatchevski construit sa géométrie, remplaçant le cinquième postulat d’Euclide par la possibilité de faire passer par un seul point une infinité de parallèles à une droite. Il concrétise alors cette géométrie sur la pseudosphère, surface de révolution établie à partir de la tractrice, courbe aux propriétés étonnantes. La tractrice
La tractrice de formule Sa principale particularité est que la longueur de la
tangente à l’axe des abscisses en tout point est constante, comme le montre le
schéma ci-dessous.
On a La pseudosphère est la
surface de révolution engendrée par la rotation d'une tractrice
autour de son asymptote. La pseudosphère a donc
une courbure négative constante. Mais comment établir le plus court chemin sur
cette surface ? Comment faire de la géométrie, que représentent un cercle,
une droite ? La géométrie sur la
pseudosphère
La courbure négative constante
permet donc d’établir dans cette géométrie une loi bien particulière : la
somme des angles d’un triangle est inférieure à deux droits, soit 180°. Ceci
est donc en contradiction avec la géométrie euclidienne… d’où le nom de géométrie
non euclidienne !
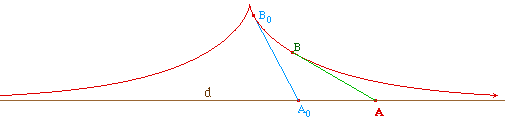
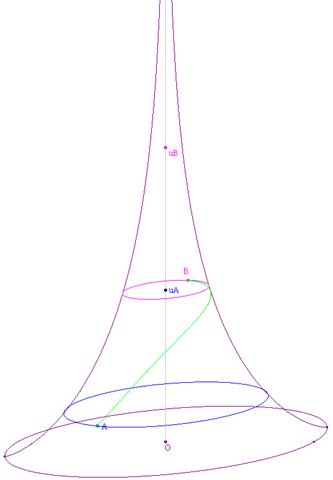
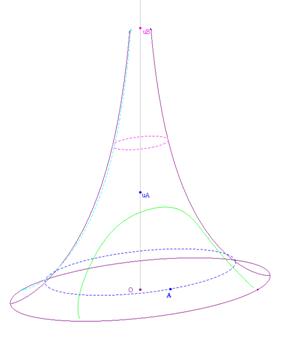
Le chemin AB le plus
court est ici symbolisé par le chemin vert. Que
représentent une droite ou un cercle sur une telle surface ?
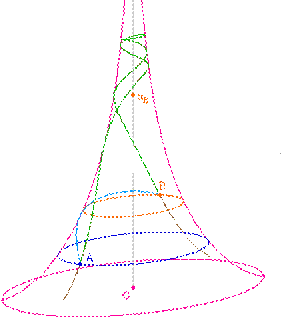
Il existe donc plusieurs
droites passant par deux points sur cette surface. Néanmoins une seule et une
unique reste la plus courte. Cette démonstration a été faite par des chercheurs
et mathématiciens français mais relève pour nous d’une bien trop haute
complexité ! Un espace… courbe ?Cette géométrie ainsi que toutes
les autres fondées à partir du 19ème siècle permettent l’étude de
notre univers, où certains savants ont constaté que les grosses masses
« courbent » l’espace dans lequel ils évoluent. La plupart des
phénomènes comme les trous noirs, la fameuse croix d’Einstein (5 points
lumineux représentant pourtant une seule et même galaxie) ont
été en partie élucidés. Les grosses masses fonctionnent à la manière de ce que
l’on pourrait appeler des lentilles gravitationnelles qui peuvent renverser,
déformer, multiplier, agrandir ou rapetisser l’image d’un astre
« transportée » par la lumière. Comprendre notre univers implique donc l’acceptation et la compréhension d’une géométrie différente de la nôtre.
Einstein fut un des précurseurs dans la
découverte des mystères de notre univers
| |